成長率一定のキャッシュフローの割引現在価値の合計
投資の世界は数字の世界なので、有名な定理や公式がたくさんある。今回は、それらの中で、筆者が「投資を考える上で最も役に立つ数式」だと思っている簡単な公式を紹介する。
それは、一定の率(g)で成長する無限遠まで続く将来のキャッシュフロー(E)を、一定の割引率(r)で割引現在価値に引き直した合計値(P)を与える公式だ。
将来のキャッシュフローに「E」、割引現在価値の合計に「P」を当てたのは、それぞれ「(一株当たり)利益」と「株価」を意識したものだ。株式を例に考えてみて欲しい。
図 1 「役に立つ公式」とその変形
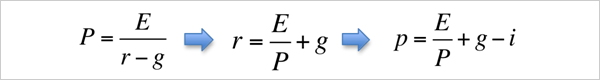
(※ pはリスク・プレミアム、iは金利)
たとえば、今期の一株当たり利益が100円で、利益成長率が2%の将来利益を、7%の割引率で評価して全て合計して求めた現在の株価は、100÷(0.07-0.02)=2000なので、2,000円となる。
ここで用いる大きな単純化は、将来成長率が一定という仮定だ。これは、将来、一様ではなく変動するはずの利益成長率を「イメージとして」架空の均一な成長率にまとめたものだ、と考えることにしよう。
尚、割引率は、分析の必要に応じて、金利(i)とリスクプレミアム(p)に分解して考えると便利だ。
株価を将来のキャッシュフローの割引現在価値として考える場合、よく登場するのは、通称「DDM」(Dividend Discount Model)こと配当割引モデルだが、利益の割引現在価値として株価を考えても本質的には同じであり、両者の差は成長率の差で吸収される。たとえば、利益の一部だけを配当している多くの会社の場合、利益を配当するよりもビジネスに再投資する方が成長率が高く、また、将来、配当性向を上げる余地がある分、利益全体を割り引くモデルよりも、分子は小さくなるが、その成長率はより大きく評価できる。
個々の銘柄を評価する場合、上記の考え方でもDDMでも、特別な成長率が続く期間とその成長率が重要になったり、DDMの場合は、配当性向が変化する時期とペースが重要になったりするが、これらについて、実用に耐える程度に正確な予想をすることは至難の業だ。
多少の皮肉を許して貰うなら、これらについて誰も正確な予測などできないから、多くの証券アナリストが大きな顔をして、その職業で食べていけるのだ。
株価水準の高低判断
さて、「日本株全体の株価水準の高・低」といったレベルでものを考える場合、個々の銘柄よりも変化が均される。DDMによる個別銘柄分析の際に時々用いられるような階段状に何通りかの成長率をあてはめるというような操作は必要ない。
さて、この単純化を受け入れると、次のようなことがいえる。先ず、株式が株主に自然に支払うことが出来るリターン(割引率であり期待リターンでもある)は、益利回り(E/P、PERの逆数に当たる)に成長率を加えた利回りだ。
次に、割引率を金利とリスク・プレミアムに分解すると、リスク・プレミアムの大きさは、益利回りと成長率の和から金利を差し引いたものとして求めることが出来る。
過去の本連載でも書いたことがあるが、筆者は、益利回りを、東証一部平均の今期PERから逆算して求め、成長率には日本の名目GDPの予想成長率を代入し、金利には長期金利(10年国債利回り)を当てはめて、長期債に対する株式のリスク・プレミアムを概算し、その大小で、大まかな株価水準の高・低を判断することにしている。
このようにして求めたリスク・プレミアムが、「6%」なら「株価は普通」、「7%」なら「株価は安い」、逆に「5%」なら「株価は高い」と判断するくらいが、目下の株価に対する高低感だ。
たとえば、バブル後半の1988年末の数字を見ると東証一部の平均PERは58.4倍なので益利回りは1.7%、名目成長率(実質成長率に消費者物価上昇率を足して求めた)は7.8%で、株式の期待リターンは9.5%になるが、当時の長期債利回りは4.7%なので、山崎式リスク・プレミアムは4.8%と5%を割り込んでおり、株価は「高い」(高すぎる確率が大きい)という判定になる。
翌1989年は、PERが70.6倍で益利回りは1.4%、名目成長率は7.7%あったが、長期債利回りは5.7%に上昇しており、山崎式リスク・プレミアムは3.4%しかなく、株価水準は前年よりもさらに割高だという判定になった。
バブルの崩壊に向き合った1990年代と2000年代の前半を通じて、日本の株式のPERは他の先進国の株式市場に近いノーマルな印象の水準になってきた。
同じ計算方法を2012年末に適用するとどうなるか。PERは18.1倍だったので益利回りは5.5%、名目成長率は2.3%だった。一方、長期債の利回りは0.8%だったので、山崎式リスク・プレミアムは7.0%となって、株価は「安い」という判定となった。
これらの例は、PERと成長率が共に「実績値」なので、実際に投資判断する場合に使うデータと異なる点で、方法の適否を評価するために使えるデータではないが、だいたいの感じは分かって頂けよう。
この方法には、いくつか使用上の注意事項がある。
先ず、「利益」は不安定なデータだ。大きなショックや天災などがあると、上場企業全体のレベルでも赤字になったり、ごく僅かなものになったりすることがある。この場合、この方法による株価判定はあまり参考にならない。
次に、「成長率」にどの数字を使うかは、絶えず悩ましい問題だ。筆者は、第一次接近として、政府が発表する予想成長率を使ってみることにしているが、民間の調査機関やIMFなどが発表する成長率と余りに大きな差がある場合や、常識的な潜在成長率やインフレ率予想から計算される名目成長率から一時的に大きく懸け離れた数字になった場合、政府予想以外の成長率を使ったり、自分で「鉛筆を舐めた」成長率を使ったりする場合がある。
もともと、一時点の成長率を恒常的な将来の成長率として使うことに無理があるのだが、他方、一般に将来の成長率のイメージは、現時点の成長率の延長として形成されやすい。ある意味では、乱暴な方法だが、大まかな一次近似として、また、定点観測的な参考データとして、時々計算してみて損はないと思っている。
また、「金利」として長期金利を考えることの適否だが、長期金利は市場で形成される金利であり、われわれが運用を考えるときの想定期間もそこそこに長いことが多いので、「リスク・フリー金利=短期金利」という通念に縛られるよりも、長期金利と株式リターンとの有利・不利を比べてみるのがいいのではないか。
株式のリスク・プレミアムが幾らなのかということは、長年、多くの学者や実務家が研究し論争してきたテーマであり、簡単ではない。
ここで述べた方法で求めたリスク・プレミアムが、正しいリスク・プレミアムの近似だと強く主張する積もりは、筆者にはない。ただ、大まかでも、株価の高・低の見当を付ける方法を持ち、実際のデータに当たってみることが大事だと思う。
尚、市場が妥当だと考えるリスク・プレミアムは、市場参加者がどのようなマーケットと損得を経験したかの「履歴」によって影響を受け、変動すると考えることができよう。たとえば、投資家の世代別のリスク・プレミアムを考えることが出来るかも知れない。「6%」が標準という、筆者が現在持っているレベル感を、硬直的に考えるべきではない。
但し、その時の状況に合わせて解釈を柔軟にし過ぎると、バブルの判定基準としての用をなさなくなる可能性があるので、「加減」というものは難しい。
株式投資とインフレ
さて、「役に立つ公式」は、株式投資とインフレの関係を考える上でも役に立つ。証券会社や運用会社がスポンサーとなるような商業的な臭いのする投資教育では、「インフレ・ヘッジになるから」あるいは「将来のインフレに対抗するために」、株式に投資すべきだと推奨(あるいは「強要」?)されることが多い。
株式投資はインフレに強いというのは、本当なのだろうか。
この問題を考えるには、先ほどの公式の「金利」と「成長率」をそれぞれ、インフレ率と実質とに分解してみるといい。図2は、これを簡単に図解したものだ。
これを見ると、分母の「割引率」と「成長率」の引っ張り合いで株価が変化することが分かるが、「インフレ率」はどちらにも共通なので、問題は、「実質金利」と「実質成長率」の引っ張り合いであることが分かる。
図 2 「役に立つ公式」をインフレ率と実質に分解
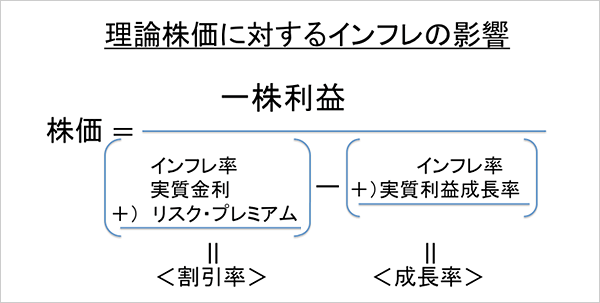
実質金利と成長率がどのように変化するのかは、その時の状況によるだろうが、インフレの初期には、金融政策が緩和的で実質金利が下がる一方、実質成長率は高まっている場合が多かろう。この場合は、両方の効果が株価にプラスに働くので、株式投資が大いに儲かることが想像できる。
他方、インフレがある程度進んで金融政策が引き締めに入る時期になると、実質金利が上昇する一方で、実質成長率が低下する局面があるだろう。最終的に金融引き締めに勝てる上昇相場はない、というのが株式投資におけるセオリーだが、この段階では、株式投資はインフレに勝つどころか、損失をもたらす可能性が大きい。
将来のインフレヘッジとしての株式投資ということを考えると、インフレの初期に大いに利益をもたらして、その後の実質価値の下落をカバーできる分まで株式投資が収益をもたらす可能性がある。この局面では、株式投資は大いに有効だ。いつまでもインフレの昂進に付き合って株式投資を続けていると、やがては損をする公算が大きい、という状況が想定できる。
ある時点で、「過去の推移を見ると、株式投資は有効なインフレヘッジになっていました」という説明を聞いて、データを見せられて納得した投資家が、株式投資を積み増しして、かえって損をするような皮肉なケースが起こりうることが分かる。
投資家にとっては、金融政策と実質金利の方向性をよく見ておくことが大切だ。



![[今週の日経平均]最高値更新も「天井サイン」出現!今週の日本株どうなる?!](https://m-rakuten.ismcdn.jp/mwimgs/6/c/160m/img_6c199645af38ea98963a94af8b6f3b6934054.jpg)










![[動画で解説]成長株、割安株、高配当利回り株…どの株を選べばいい?](https://m-rakuten.ismcdn.jp/mwimgs/8/4/498m/img_84b60a4da51373f73b5c52275b097f2837381.jpg)













![[動画で解説]桐谷さんの優待生活に突撃!#1~桐谷さん、おきに優待ベスト3見せてください!~](https://m-rakuten.ismcdn.jp/mwimgs/9/5/498m/img_9528c8c2f23001a3deb43de0c6f7845872398.jpg)





















![[今週の日経平均]最高値更新も「天井サイン」出現!今週の日本株どうなる?!](https://m-rakuten.ismcdn.jp/mwimgs/2/b/160m/img_2b5a074cc6a3e935645125fb974dffcf59165.jpg)


![[動画で解説]みずほ証券コラボ┃7月16日【米株は小型選別 日本株はドル建てに注目~今週は米共和党大会と米決算発表~】みずほウィークリーVIEW 中島三養子](https://m-rakuten.ismcdn.jp/mwimgs/2/a/498m/img_2a5df0131378bd46a83ce1f01fbb418d92438.jpg)
![[動画で解説]【テクニカル分析】今週の日本株 最高値を更新後日本株はどうなる?~出現した「天井サイン」をどう読むか~<チャートで振り返る先週の株式市場と今週の見通し>](https://m-rakuten.ismcdn.jp/mwimgs/6/0/498m/img_60df7a3c9e52ac000de20f75f870968d71371.jpg)
![[動画で解説]円高ショックで日経平均急落、夏枯れ相場始まり?](https://m-rakuten.ismcdn.jp/mwimgs/3/c/498m/img_3c55226b36153bdd05e3d3a674f68f9245072.jpg)
![[動画で解説]新NISAを使った個別株投資について](https://m-rakuten.ismcdn.jp/mwimgs/0/c/498m/img_0c14e3a2b5e84beb52872a9b879aa3e795587.jpg)

















![[今週の日経平均]最高値更新も「天井サイン」出現!今週の日本株どうなる?!](https://m-rakuten.ismcdn.jp/mwimgs/6/c/356m/img_6c199645af38ea98963a94af8b6f3b6934054.jpg)
























![[動画で解説]日銀が7月利上げに踏み切るべきでないこれだけの理由](https://m-rakuten.ismcdn.jp/mwimgs/a/8/160m/img_a8715b638366eed8a8f8d75613b8e92163161.jpg)


![[フィーチャー] バイデン氏もトランプ氏も鉄鋼業界を救いたいが、つぶす可能性もある](https://m-rakuten.ismcdn.jp/mwimgs/3/2/160m/img_32aca21472e8a9bb523a39c473740d6a30904.jpg)




